I implemented the Degree-Ordered Directed Graph (DODG) algorithm for triangle counting on undirected graphs. Prior work on this problem was based on adjacency matrix multiplication, which is slow and memory intensive. I also experimented with a parallel version of DODG algorithm and observed that it is fast and scalable.

Degree-Ordered Directed Graph

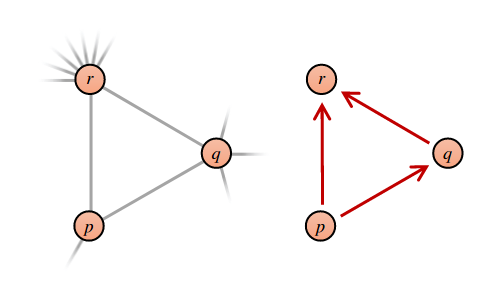
Finding triangles is basically enumerating open triads i.e, edges of the form $\{(a, b), (b, c)\}$ and checking if a closing edge $(a, c)$ is present in the graph. However, it is not necessary to check all open triads, only one per triangle is needed. The DODG approach essentially provides a vertex ordering criteria which ensures that only vertex per triangle receives two of its edges. We build a Degree-Ordered Directed graph from the original undirected graph where edges are directed from low-degree to high-degree. Edges between vertices of equal degree are directed based on a simple hashed-based tie breaking. Triangles are then counted in the DODG by considering every vertex$(u)$ as pivot and picking a pair of it’s neighbors $(v, w)$ i.e, edges $\{(u, v), (u, w)\}$ and checking if the edge $(v, w)$ exists. If $(v, w)$ is found, then the triangle count is incremented. The figure below illustrates conversion of an undirected graph (with $d_{p} < d_{q} < d_{r}$) to DODG :

Multithreaded Implementation

For the shared-memory parallel implementation, vertices in DODG are greedily partitioned into threads based on their degree and every thread only maintains the triangle count for the vertices that it owns. These counts are summed up to return the total triangle count.

Adjacency Matrix Method

If $A$ is the adjacency matrix of a graph, then the number of triangles $= trace(A^3)/6$. More efficient way to do this :

Let $C = A^2 \circ A$ , where $\circ$ denotes element-wise multiplication
then $n_{T} = \sum_{ij} (C)/6$

Benchmarks

The complete benchmarking code can be found here. Six threads were used for the parallel version.

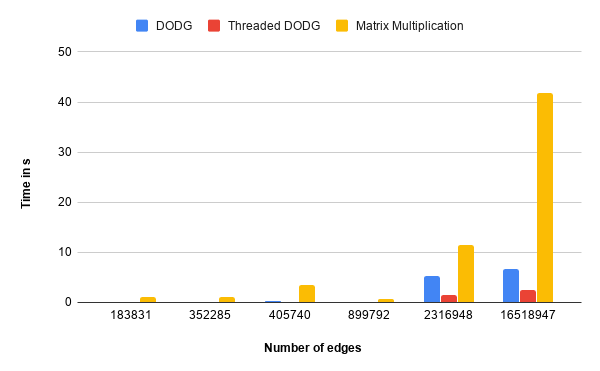
Graph	|V|	|E|	Triangles	DODG  (time in s)	Threaded DODG	Matrix Multiplication
email-Enron	36692	183831	727044	0.0474	0.0272	1.1652
cit-HepTh	27770	352285	1478735	0.1065	0.0298	1.1857
soc-Epinions	75879	405740	1624481	0.1997	0.0711	3.3931
amazon0302	262111	899792	717719	0.1382	0.0836	0.6483
flickrEdges	105938	2316948	107987357	5.3215	1.4930	11.4837
cit-Patents	3774768	16518947	7515023	6.6124	2.5186	41.7712

Results

The DODG implemenation is on average 5-10X faster than the adjacency matrix method on a single core, with a further 2-3X improvement on six cores using shared-memory parallelism.